Some notes about "What's new in Mathematica 9: Builtin R Integration"
To understand what's going on, please open the example: Hierarchical Clustering.
This posting is basically about how to integrate R via Rpy2 in Python and hence also in Sage.
First thing you should notice is the clash of two parallel worlds. MMA's "RSet" command converts and sets the variable y in the scope of R. That's nice, but wouldn't it be much easier, to just have a local variable for that? Second of all, the function definitions inside strings - filled with escaped quotes - is also not that great. Isn't there are better quoting available?
What I want to do is to accomplish something similar with Rpy2. So yes, there are also equivalents to this RSet function, and you can also evaluate arbitrary R code inside strings (Python has triple-quoting to avoid escaping quotes). But that's not everything. You can import R packages [from rpy2.robjects.packages import importr] and bind them to local variables and have, for example, tab-completion on them. R Functions can be referenced directly, data-sets can be exchanged with implicit converters (e.g. numpy's ndarray -> R's Matrix), etc.
You can see the final output and code here: https://gist.github.com/4176508
Besides the usual import/from stuff common in Python, I start by creating a random matrix with Numpy:
mdata = np.random.randn(10, 5)
Enable autmatic conversion between Numpy and R:
from rpy2.robjects import numpy2ri
numpy2ri.activate()
Print the matrix using R's print:
rprint = robj.globalenv.get("print")
rprint(mdata)
[,1] [,2] [,3] [,4] [,5]
[1,] 2.1844065 -1.05401295 1.18316261 -0.356338229 1.55031790
[2,] 1.2476473 0.89507075 -0.14576584 0.006899727 0.01350773
[3,] -1.6416017 -0.28180113 0.02784612 1.199042583 0.01272994
[4,] 1.8645490 0.30993270 0.18107913 0.131505590 0.57083588
[5,] 1.2397427 0.73639680 -0.42883124 -0.436741492 0.43644592
[6,] -0.1980955 -0.04463804 -0.11217381 1.768415923 -1.82884840
[7,] 0.2943145 2.12648235 0.21068166 1.718289719 0.15711455
[8,] 0.2453526 0.64922040 1.80518277 0.086208024 1.18789962
[9,] 0.8229507 0.56227084 -1.72153433 -1.511514201 1.04610492
[10,] 0.1430900 0.03371198 -0.58992825 1.023002088 -1.47153121
... and just for fun, R'summary, printed with Python's print function:
print r.summary(mdata)
V1 V2 V3 V4
Min. :-1.6416 Min. :-1.05401 Min. :-1.72153 Min. :-1.5115
1st Qu.: 0.1687 1st Qu.:-0.02505 1st Qu.:-0.35806 1st Qu.:-0.2655
Median : 0.5586 Median : 0.43610 Median :-0.04216 Median : 0.1089
Mean : 0.6202 Mean : 0.39326 Mean : 0.04097 Mean : 0.3629
3rd Qu.: 1.2457 3rd Qu.: 0.71460 3rd Qu.: 0.20328 3rd Qu.: 1.1550
Max. : 2.1844 Max. : 2.12648 Max. : 1.80518 Max. : 1.7684
V5
Min. :-1.82885
1st Qu.: 0.01292
Median : 0.29678
Mean : 0.16746
3rd Qu.: 0.92729
Max. : 1.55032
... now applying the labels. This time, I show how to execute R code directly, hence injecting the variable "y" in R's global namespace, too:
from rpy2 import robjects as robj
robj.globalenv['y'] = mdata
r("""
dimnames(y) <- b="b">list(paste("g", 1:10, sep=""),
paste("t", 1:5, sep=""))
y
""")
Compare this to the way you have to do this in MMA9!
--- EDIT
Below is a way how the same is accomplished in Python. The paste command is replaced by Python's list comprehension, the list command is from R and mdata is converted to an R object to be able to do slot assignments.
mdata = numpy2ri.numpy2ri(mdata)
import rpy2.rinterface as ri
descr = ri.baseenv["list"](
ri.StrSexpVector(['g%s'%_ for _ in range(10)]),
ri.StrSexpVector(['t%s'%_ for _ in range(5)]))
mdata.do_slot_assign("dimnames", descr)
The first example is certainly more pleaseant, but once you would create some neat aliases for the R functions (e.g. list = ri.baseenv["list"]; strv = ri.StrSexpVector; ...), working in Python shouldn't be hard, too.
--- END EDIT
Calculating the correlation and distance matrix. Notice, that dots in R's functions, like the as.dist(), are converted to underscores in Python. Those dots are just like normal letters in the identifier name, nothing further.
stats = importr("stats")
corrm = r.cor(r.t(mdata), method="spearman")
# no idea how to do 1-matrix automagically
robj.globalenv['corrm'] = corrm
distm = stats.as_dist(r("1-corrm"))
rprint(corrm)
rprint(distm)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1.0 -0.3 0.1 0.5 -0.2 0.9 0.8 0.6 0.3 0.2
[2,] -0.3 1.0 0.6 0.3 0.7 -0.4 0.0 0.1 0.2 -0.5
[3,] 0.1 0.6 1.0 -0.1 -0.1 -0.3 -0.1 0.7 0.6 -0.9
[4,] 0.5 0.3 -0.1 1.0 0.7 0.6 0.7 -0.1 -0.3 0.3
[5,] -0.2 0.7 -0.1 0.7 1.0 0.0 0.3 -0.4 -0.3 0.2
[6,] 0.9 -0.4 -0.3 0.6 0.0 1.0 0.9 0.3 0.1 0.6
[7,] 0.8 0.0 -0.1 0.7 0.3 0.9 1.0 0.4 0.3 0.5
[8,] 0.6 0.1 0.7 -0.1 -0.4 0.3 0.4 1.0 0.9 -0.4
[9,] 0.3 0.2 0.6 -0.3 -0.3 0.1 0.3 0.9 1.0 -0.3
[10,] 0.2 -0.5 -0.9 0.3 0.2 0.6 0.5 -0.4 -0.3 1.0
1 2 3 4 5 6 7 8 9
2 1.3
3 0.9 0.4
4 0.5 0.7 1.1
5 1.2 0.3 1.1 0.3
6 0.1 1.4 1.3 0.4 1.0
7 0.2 1.0 1.1 0.3 0.7 0.1
8 0.4 0.9 0.3 1.1 1.4 0.7 0.6
9 0.7 0.8 0.4 1.3 1.3 0.9 0.7 0.1
10 0.8 1.5 1.9 0.7 0.8 0.4 0.5 1.4 1.3
The clustering happens below (note: I had to execute the "NULL" in the r context, because it seems that Python's "None" isn't converted)
hr = stats.hclust(distm, method = "complete", members = r("NULL"))
Plotting is straightforward too. To plot to a device besides X11, one has to be a bit more specific. The documentation is full of examples. Notice, the only special part is the mfrow=r.c(1,2).
Looking at Wolfram's blogpost, I really don't want to understand what MMA's "getRPlot[...]" calling "mathematicaRPlotWrapper" does.
grdevices = importr('grDevices')
grdevices.png(file="mma9rpy2.png", width=512, height=300)
try:
r.par(mfrow = r.c(1,2))
r.plot(hr, hang = 0.1)
r.plot(hr, hang = -0.1)
finally:
grdevices.dev_off()
grdevices.png(file="mma9rpy2-2.png", width = 512, height = 512)
try:
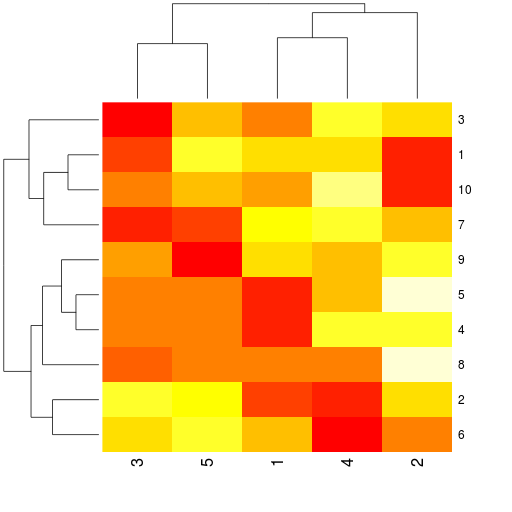
r.heatmap(mdata)
finally:
grdevices.dev_off()
Final results:
... and a heatmap plot:
Final note, yes I know there is some fuzz at the bottom of the image with the dendrogram. I don't know why. Maybe someone can fix this ... and yes, that's possible, because all of this is fully open-sourced :-)
td;dr: https://gist.github.com/4176508